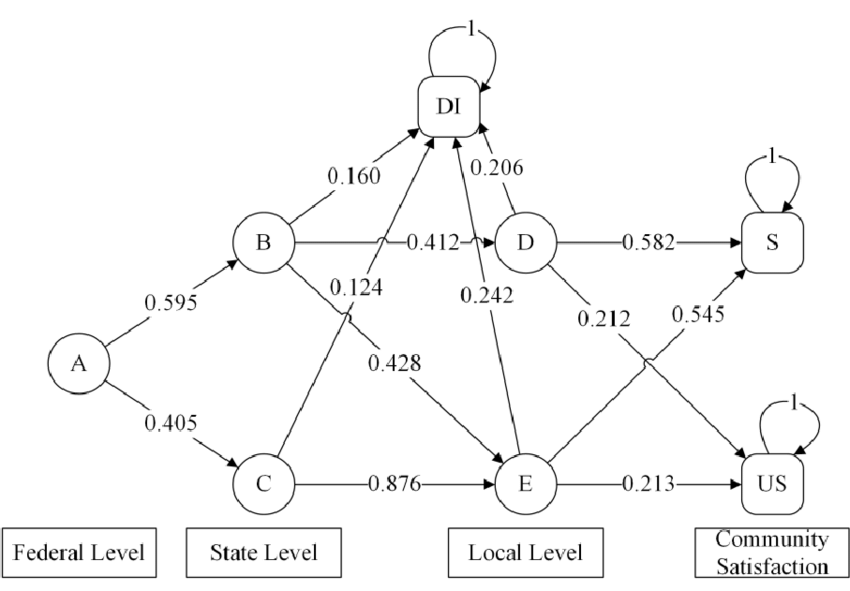
Absorbing Markov chains are a specific type of Markov chain where at least one state cannot transition to any other state outside of itself. This means that the chain will eventually reach this state and become “absorbed” into it, unable to move to any other states. Moreover, A state of a Markov chain is absorbing if it is impossible to leave it, i.e. the probability of leaving the state is zero, and a Markov chain is labeled ‘absorbing’ if it has at least one absorbing state. A Markov chain is the state in which one gets stuck forever.
Block Matrix
One important property of absorbing Markov chains is that they can be represented as a block matrix in which the absorbing states form the bottom right block. This matrix is called the “fundamental matrix” and is used to calculate the expected number of steps required to reach an absorbing state, given that the chain starts in a particular state.
Classification of Absorbing Markov Chain
Additionally, absorbing Markov chains can be classified into different types based on their structure. A type is considered “regular” if there exists a positive integer k such that all entries of the kth power of the transition matrix are positive. This means that the chain will eventually reach an absorbing state with probability. Another important property of absorbing Markov chains is the notion of “recurrence” and “transience”. A state is considered “recurrent” if, once the chain reaches that state, it will return to that state with probability 1. A state is considered “transient” if, once the chain reaches that state, there is a nonzero probability that it will never return to that state. Overall, absorbing Markov chains is a powerful tool in modelling various processes, such as epidemic spreading or financial market dynamics. By understanding their properties and structure, we can gain valuable insights into the behaviour of complex systems. An absorbing Markov chain is one with has/have absorbing states, and with the help of some finite number of steps, it is possible to move from a transient state to an absorbing state.
Elaboration
Thus, an absorbing Markov chain is one with t transient states and s absorbing states, and can be debated as P, given as under :
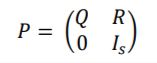
Such that, Q denotes a t x t matrix, R is a t x s matrix, 0 is a s x t zero matrix, and Is is the s x s identity matrix. Once an absorbing Markov state is attained, it cannot be left. It can be further explained using the following transition matrix-

In the above matrix, the second or middle state is an absorbing state, since the probability to transition from the second state to second state remains 1. Moreover, the probabilities to move from the second to third or first states is 0, denoting that it will continue to stay in Ss, with a probability of 1. Thus, if a variable is in the second state, it will remain there. From the above matrix, it can therefore, be implied that if a probability of column i and row i, then pii, is 1, then it will denote the absorbing state.
There is also a possibility to have more than two absorbing states in a matrix. For instance-

In the above matrix, both the S2 and S3 are in absorbing states, since the probability to remain in same state is 1, and the probability to shift to another state is 0. While these states are called absorbing states, the other states are known as transient states. Like in the above matrix, S1 is transient state.