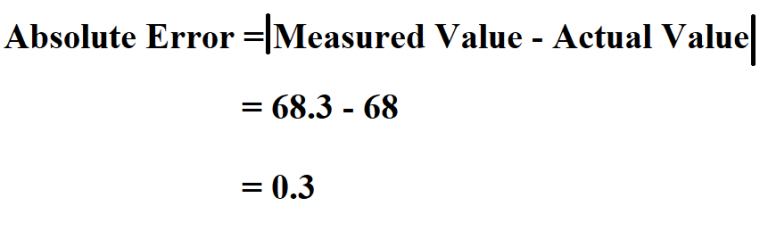The concept of absolute error is fundamental in the field of statistics and measurement. It refers to the difference between the observed value of a variable and its true value, or in other words, the degree of accuracy or precision of the measurements taken. This error can be positive or negative, depending on whether the observed value is greater or lesser than the true value. The absolute error, however, is always positive, as it corresponds to the absolute difference between the two values. The absolute error is often measured in the same units as the variable being observed or measured, such as meters, seconds, or degrees Celsius.
Calculation of an Absolute Error
It can be calculated using a formula that subtracts the observed value from the true value and takes the absolute value of the difference. This provides a measure of the magnitude of the error without regard to its direction. It is important to note that the true value of a variable is often unknown or impossible to determine with absolute certainty, making the estimation of the absolute error a crucial step in many scientific and engineering applications.
Uses of Absolute Error
The absolute error can be used to establish the quality of the measurements taken and to evaluate the performance of instruments or devices used in the measurement process. Moreover, absolute error is a key factor in making decisions about statistical significance. By knowing the absolute errors associated with observations, measurements, and experiments, scientists and researchers can determine whether the differences between two variables are statistically significant or merely due to chance. In this way, absolute error serves as an essential tool for drawing accurate and reliable conclusions about the data collected. The absolute error of an observation x is the absolute deviation of x from its “true” value.
Formula
It is calculated by taking the difference between the measured and the deviated value of a quantity, x1, and the actual value, say x0. The formula for absolute error is given as under-
Δ𝑥 = 𝑥1 − 𝑥0
The value of absolute error, however, depends on the measuring quantity. For instance, when checking the experiments on medicines compositions, the absolute error value of 0.1 makes a huge difference, while the same value of absolute error is negligible, in measuring the distance between two destinations. It is due to this fact that sometimes, absolute values are considered inadequate in finding the importance of the error.
Example
As example of absolute error can be stated as follows. If a scale post-experiment shows the value of 90 mm, while the actual value is 89.6 mm, then the absolute error for the scale is 90 = 89.6, which is 0.40 mm.
Classification of Absolute Error
One can further classify absolute error into the following three categories-
Absolute accuracy error- It is the other name of absolute error, and is found by calculating the difference between the experimental value and actual value.
𝐴𝑏𝑠𝑜𝑙𝑢𝑡𝑒 𝐴𝑐𝑐𝑢𝑟𝑎𝑐𝑦 𝐸𝑟𝑟𝑜𝑟 = 𝐸𝑒𝑥𝑝 − 𝐸𝑡𝑟𝑢𝑒
such that 𝐸𝑒𝑥𝑝 is the experimental value and 𝐸𝑡𝑟𝑢𝑒 is the actual or true value.
Mean Absolute Error (MAE)- MAE is the average of all the values of absolute errors calculated. It is found using the following formula-
𝑀𝐴𝐸 = 1𝑛∑|𝑥𝑖 − 𝑥| 𝑛𝑖=1
Such that, 𝑥𝑖 is the measured value for i observation, while x is the actual value.
Absolute Precision Error- it is computed as the standard deviation of the number group and helps to learn the magnitude of spread in the data.